Making Sense of the Monty Hall Problem! 🎲

Using code to prove outcomes that don't seem very obvious or intuitive.

Hi everybody - today, we are going to look at how code can help us make sense of outcomes that seem a bit counterintuitive. To help explain this, we are going to look at the classic Monty Hall Problem that has puzzled a lot of people for many years.

Pre-read: The Monty Hall Problem

Before we get into it, If this is your first time hearing about the Monty Hall Problem, take a few moments to read all about it in my latest article:

I walk through how the game is played, how Monty tries to help, and the logic behind why the contestant must always switch to the door Monty leaves behind to win. Knowing the details here will help make the rest of the content more relatable.

Probabilities can Concentrate

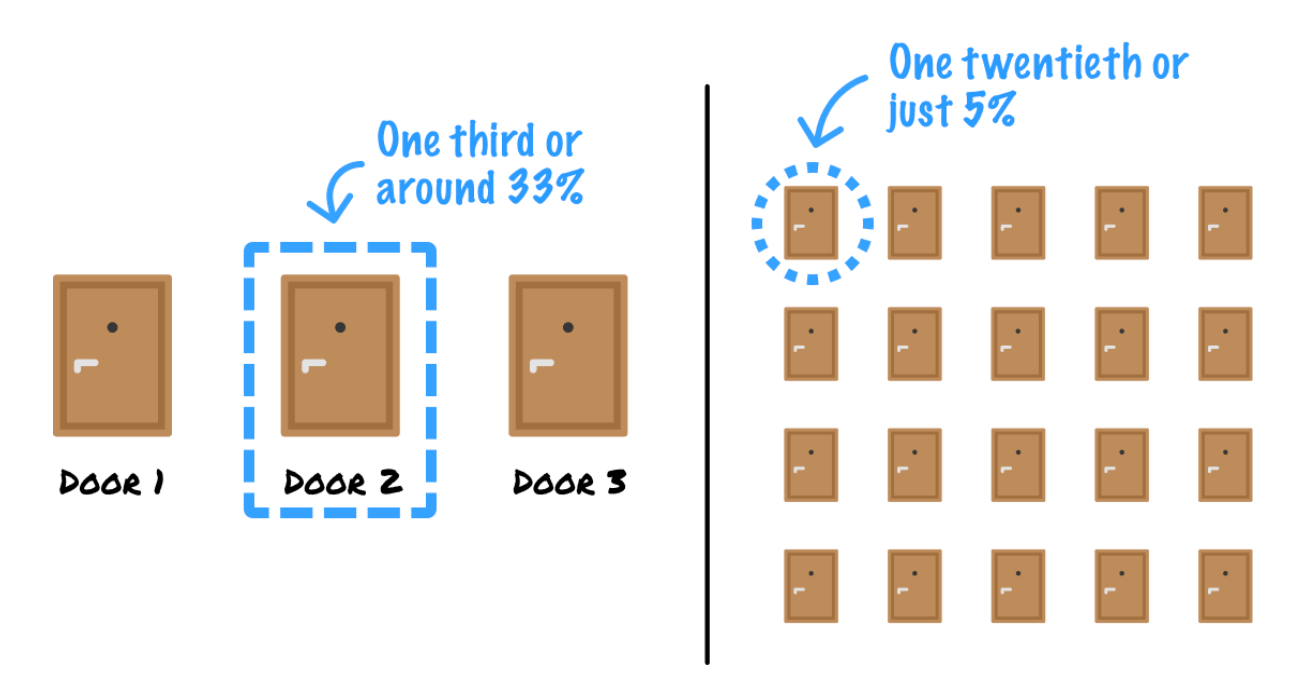
The main aha! moment when playing this game is that the contestant starts off randomly guessing, which gives them a very low chance of choosing the winning door:

The contestant does have a high-probability winning path. That path reveals itself when Monty helps out by eliminating a lot of doors that contain low-value items. In the end, the contestant is left with just two doors, where one door is the one that they chose at the very beginning. The other door is the one that remains after Monty eliminated a bunch of bad choices.

The counterintuitive aha! part is that the probability of choosing the winning door greatly increases when the contestant switches away from their initial selection and chooses the door Monty presents.

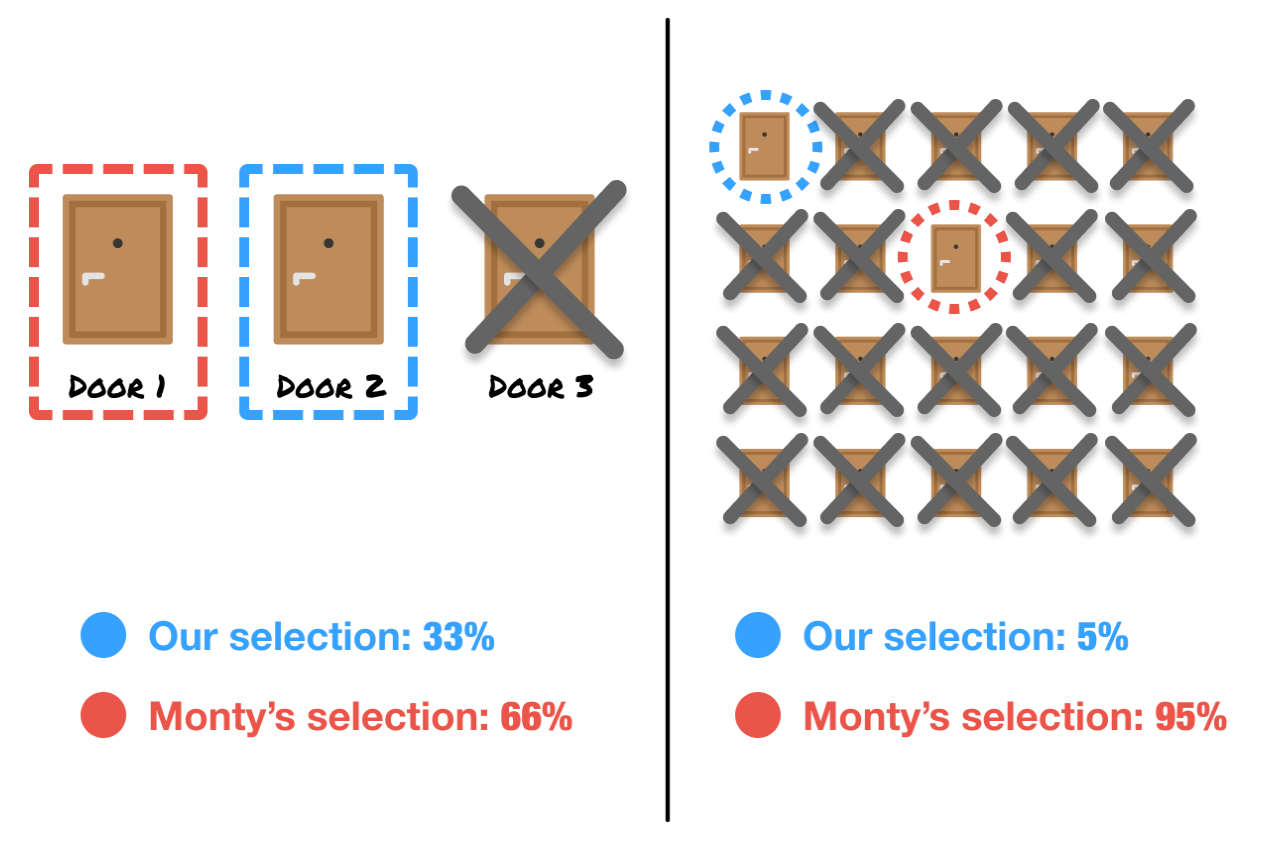
How high is the probability of winning? When Monty comes in and eliminates almost all of the low-value doors, the probability of the single remaining (unselected) door storing a high-value item remains the same as it was when we looked at all the doors in aggregate that the contestant didn’t select:

That seems counterintuitive, but that is because probabilities can concentrate when there is added information. The added information here is that Monty’s chosen door comes from a region of doors that all had a higher probability of housing the winning door than the contestant’s initial random guess. That is why the winning strategy is to always switch to the door Monty gives us.

Simulating the Strategy with Code

When we look at these diagrams and reason out the probabilities, it theoretically makes sense why switching to the other door after the initial guess is the right thing to do. To truly make this all real, we can simulate the Monty Hall Problem using code and see the output for ourselves.

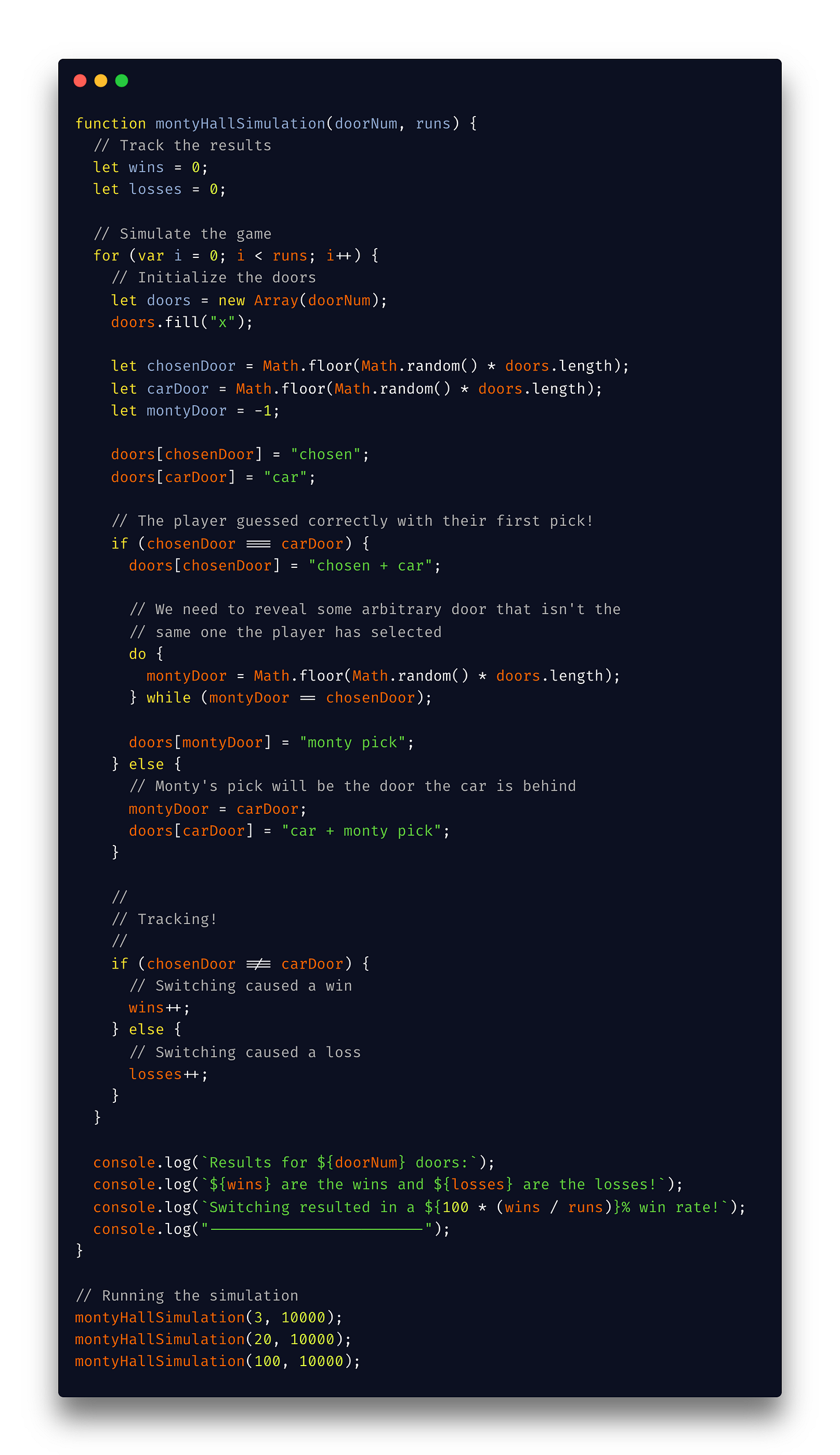
You can view the copy/paste-able code here, but here is an image of what our code looks like:

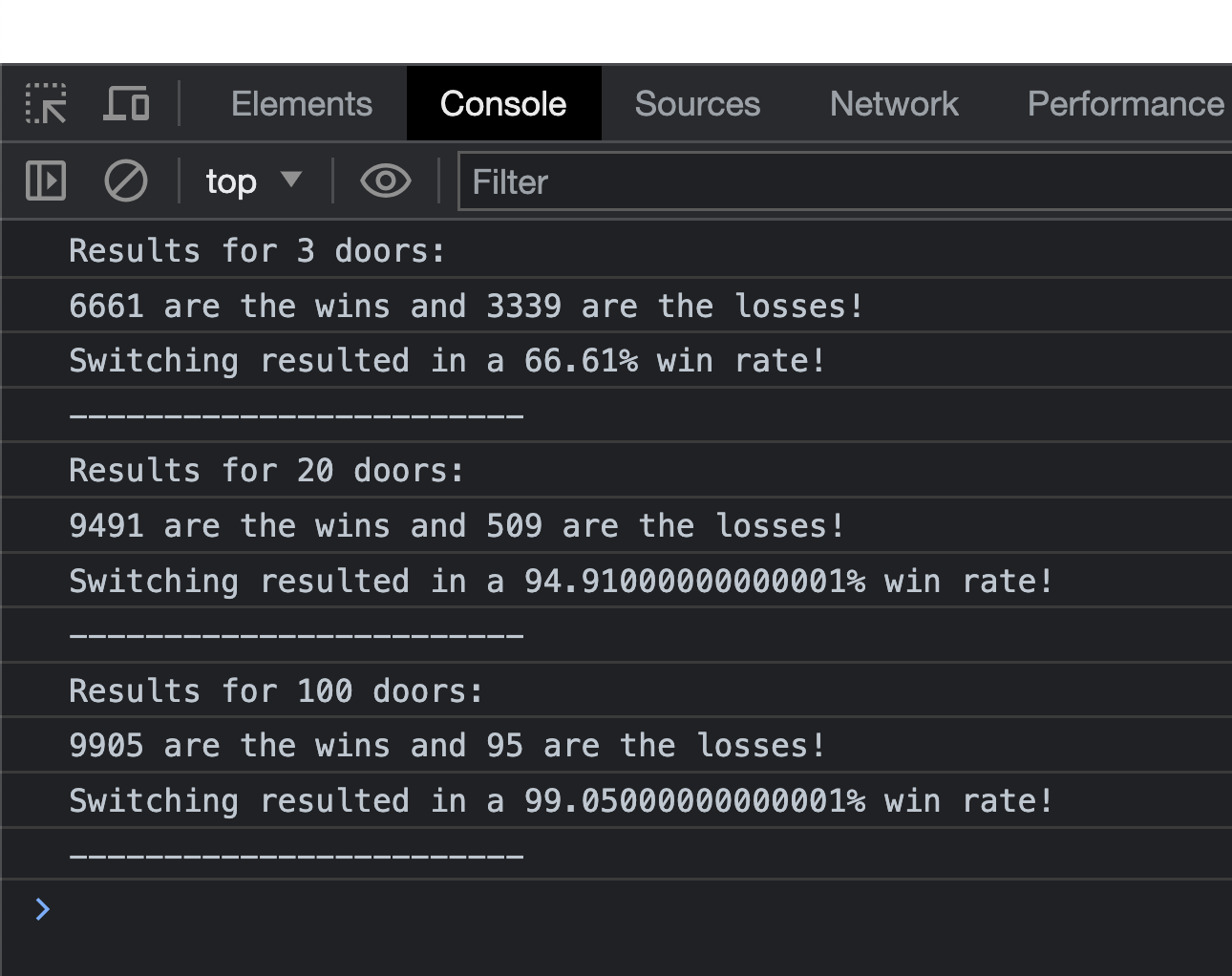
In this code, we run a 10,000 iteration simulation for what happens when we play the Monty Hall Problem with 3 doors, 20 doors, and 100 doors. The output looks as follows:

Notice how the real-world numbers very closely match the numbers we predicted in our Monty Hall Problem deep-dive. For three doors, switching resulted in a win rate of around 66%. For 20 doors, switching resulted in a winning rate of around 95%. For 100 doors, the win rate was around 99% when switching. Really cool, right?

Until Next Time

Hopefully, you enjoyed by random deep dive into the Monty Hall Problem. There are many cases, at least for me, where number theory and probability puzzles make more sense when I see them working in real life. By writing some code and simulating the outcome of those puzzles, a lot of the mystery is removed. The problems we are solving become more real.

If you have a favorite mathematical puzzle whose answer seems confusing, let me know in the comments below or by posting on the forums!

Cheers,
Kirupa 😇