Easily Draw Any Polygon! 🏜️
Let's look at a generalized approach for drawing some of our favorite shapes!
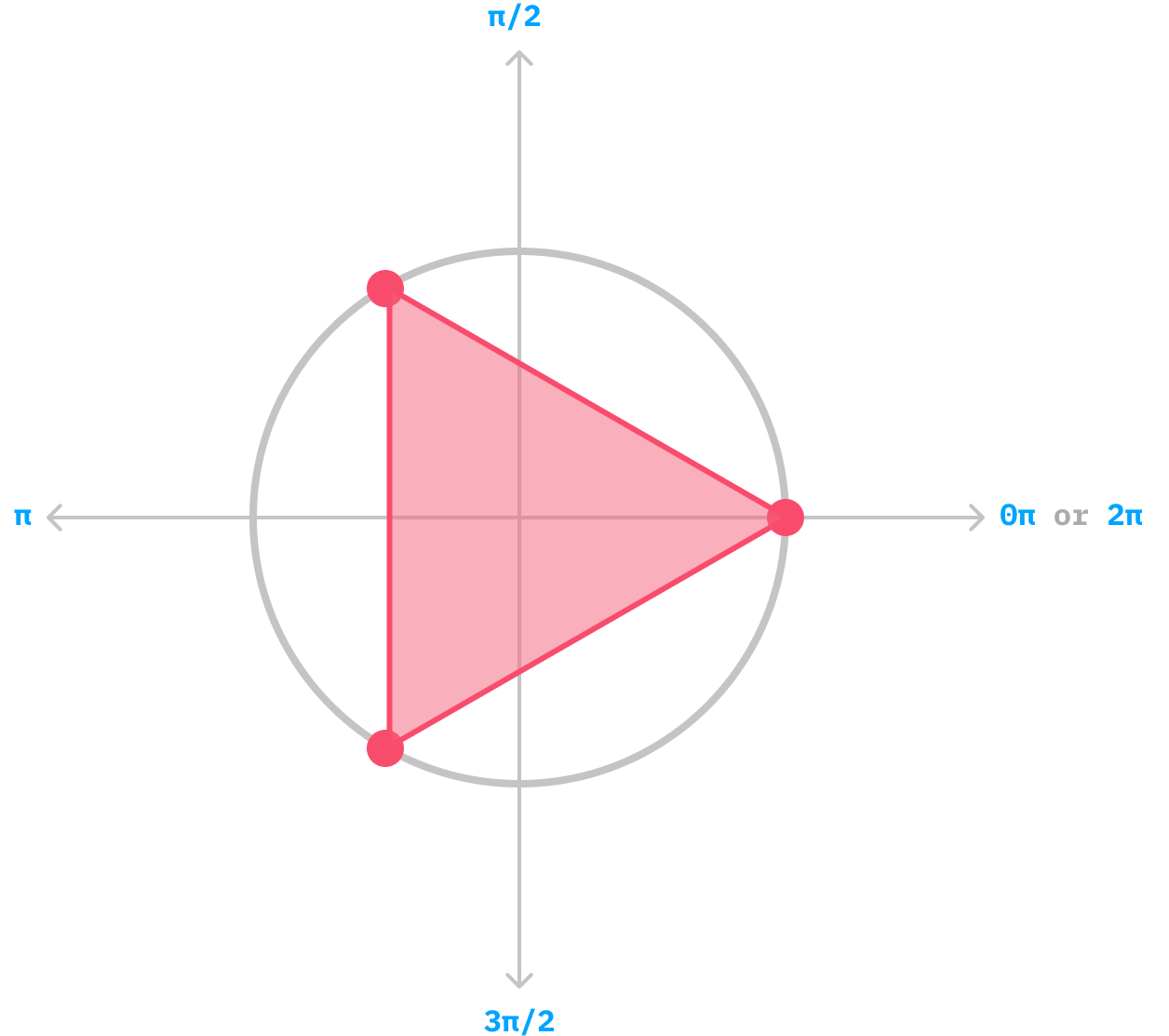
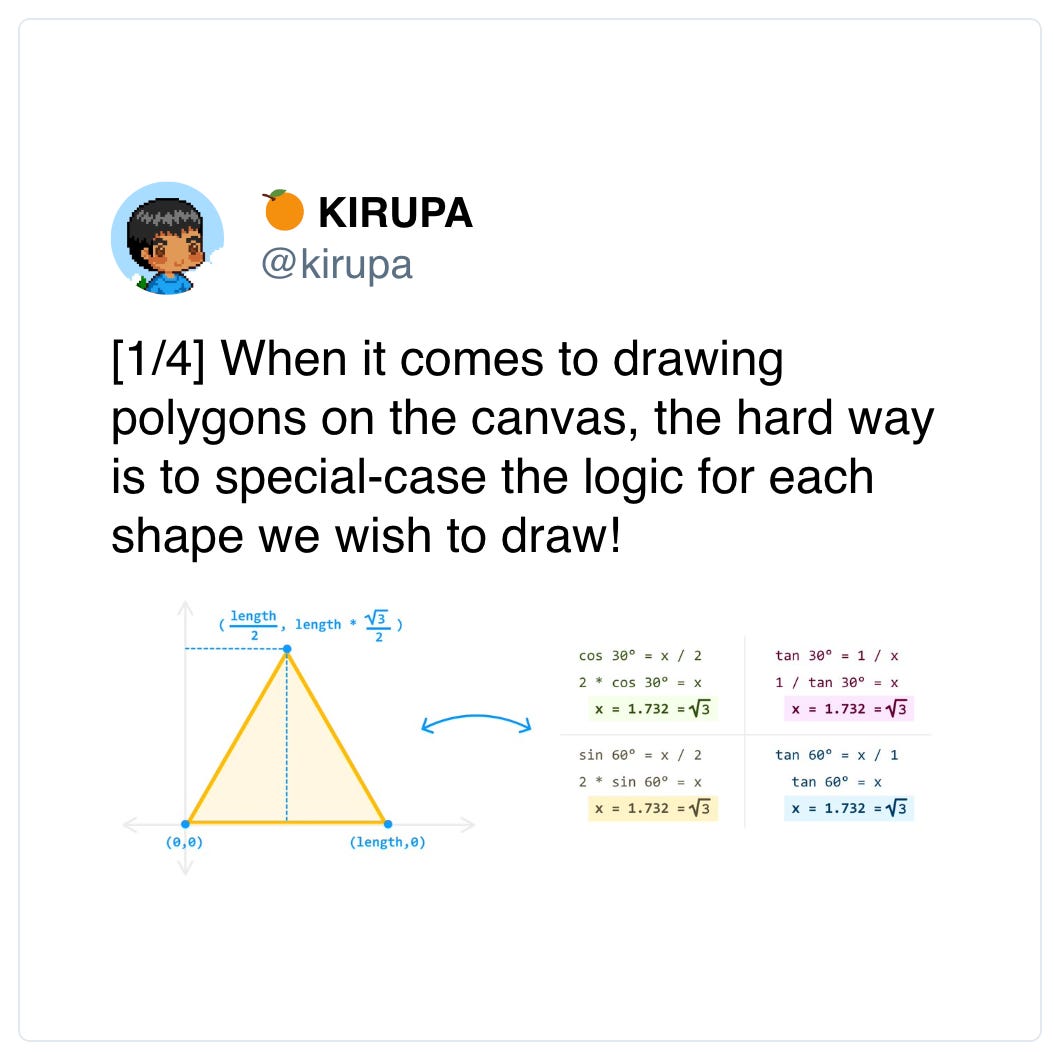
Hi everybody - there are two ways to draw polygons on the canvas. There is the hard way, which is what we looked at in an earlier tutorial where we learned how to draw a triangle (and only a triangle!):
And then there is the easy way where we use a generalized approach to draw any polygon.
The Generalized Approach
In our generalized approach, we draw our polygons by mapping our shape’s number of points (aka vertices) onto equally spaced positions on a virtual circle:
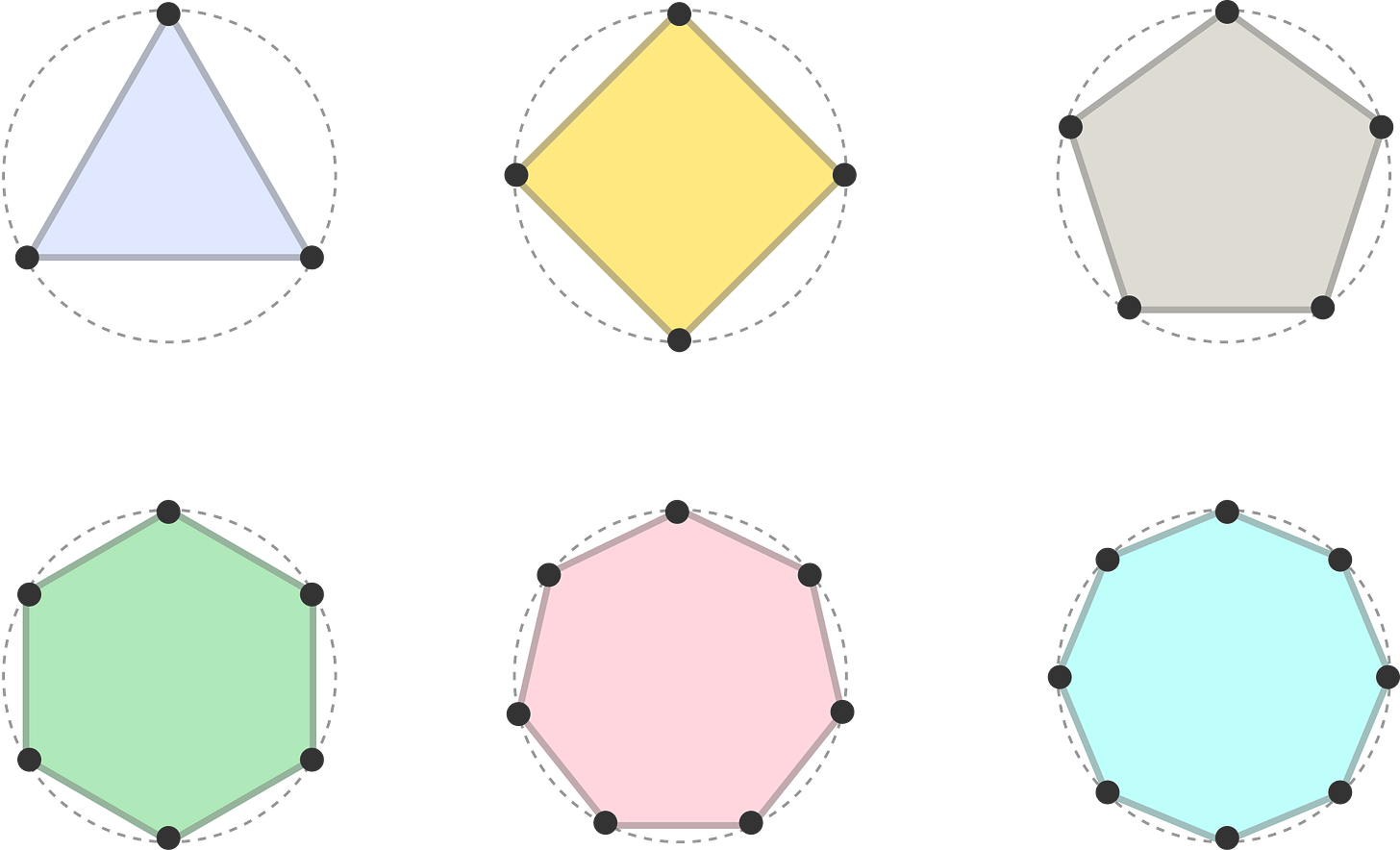
This approach works for our triangle as well as any other shape we may wish to draw:
Notice that each vertex is positioned on this virtual circle. This all probably doesn’t make a whole lot of sense, so let’s walk through an example where we draw a pentagon using this approach:
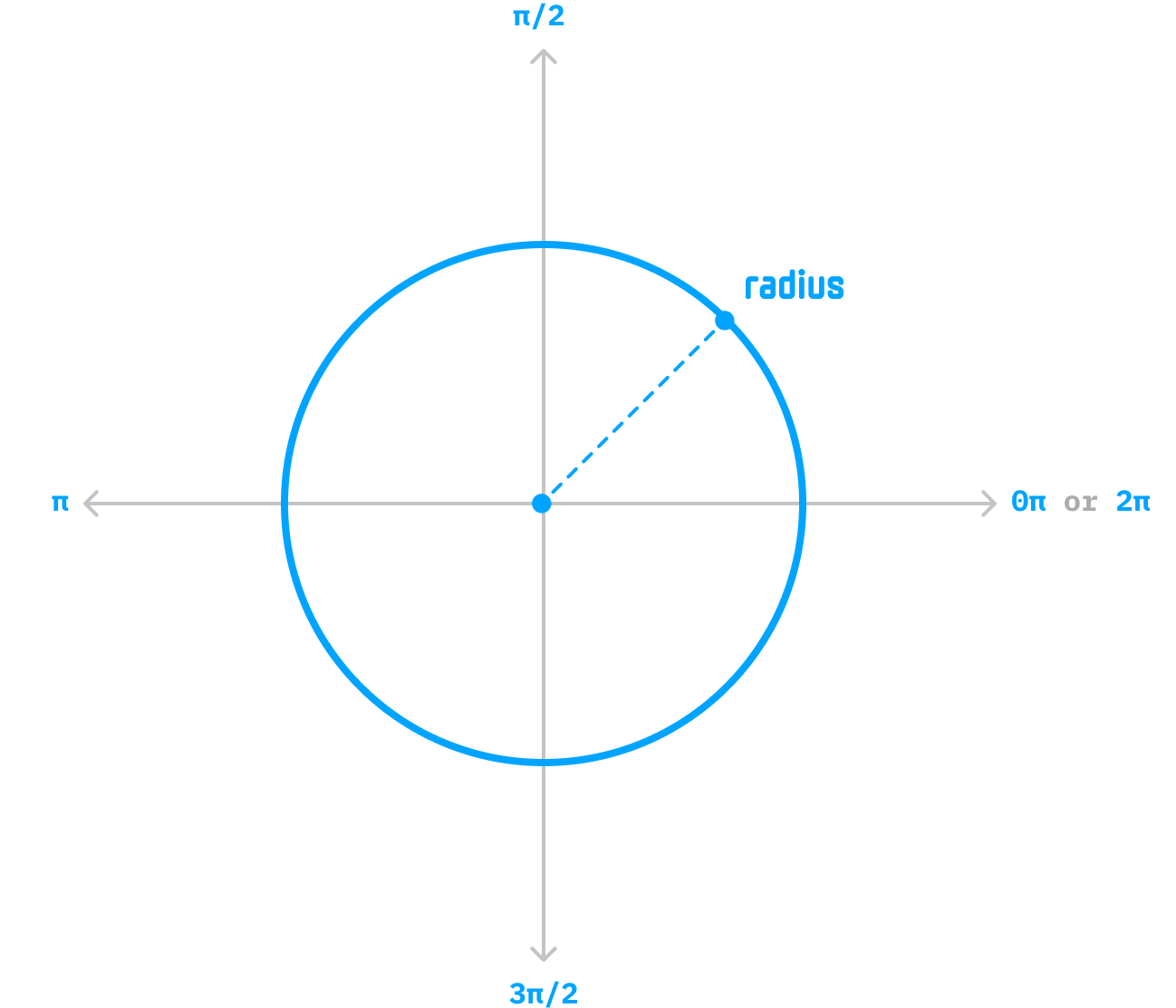
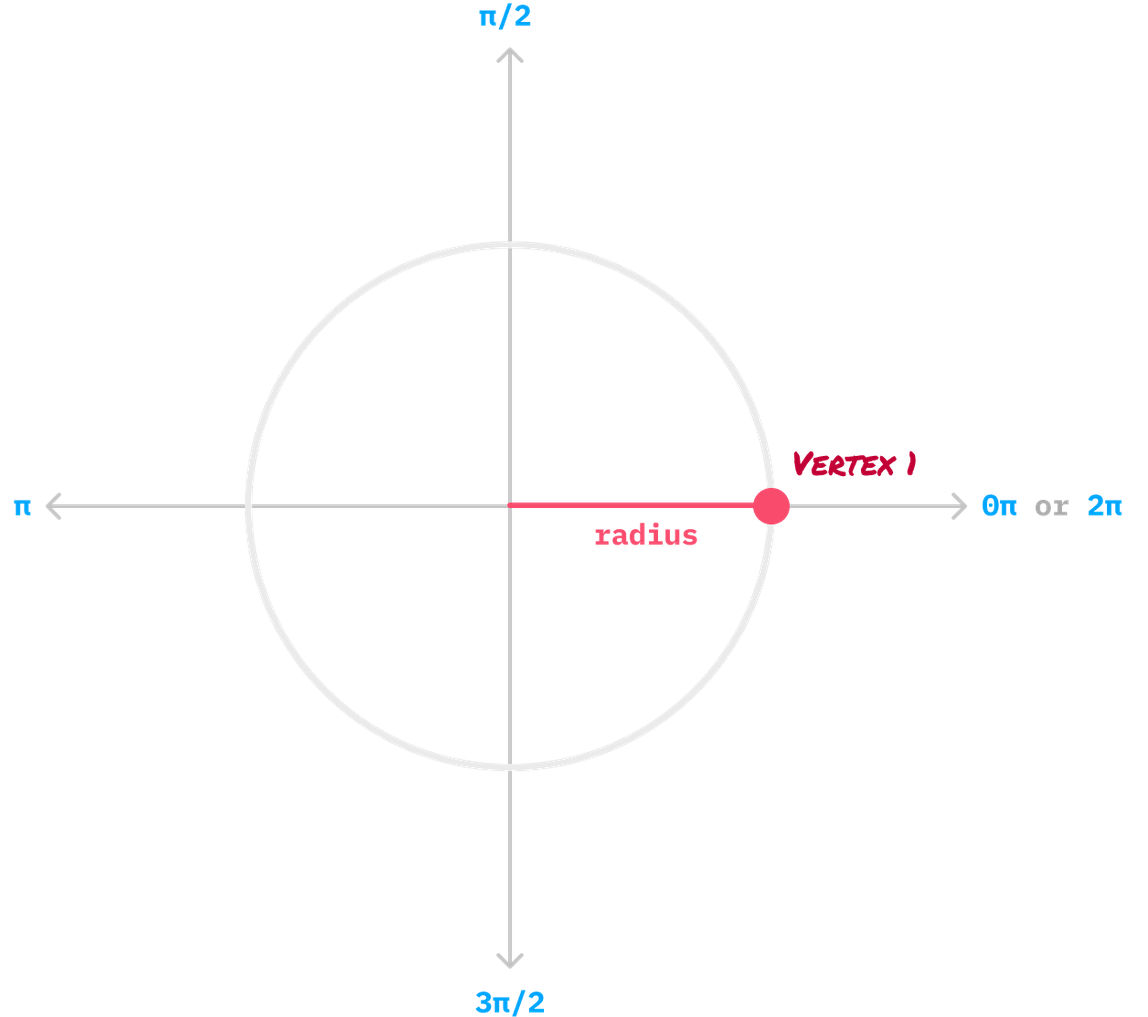
The way we can draw our pentagon is by first thinking about our shapes as series of vertices on our virtual circle whose size is determined by the circle’s radius:
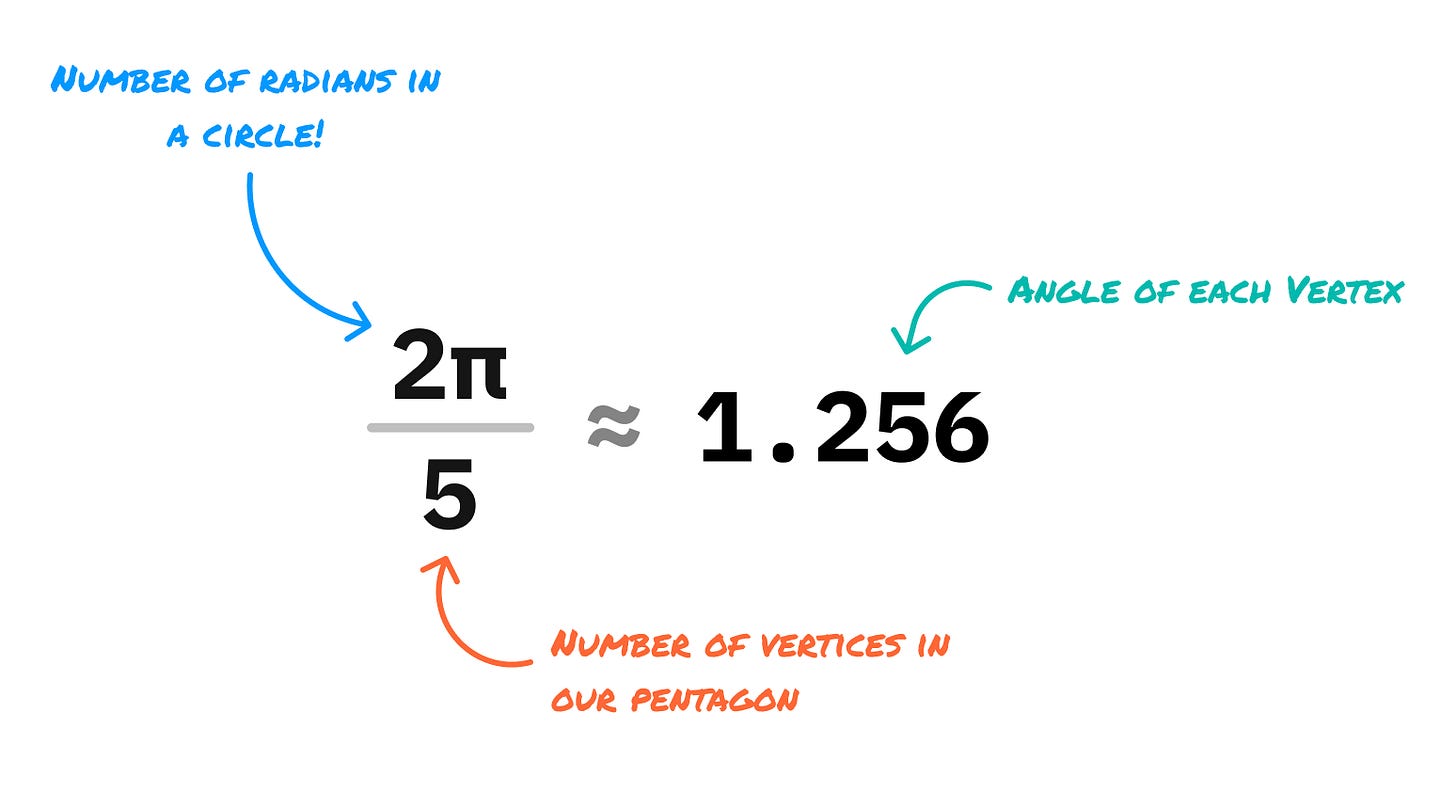
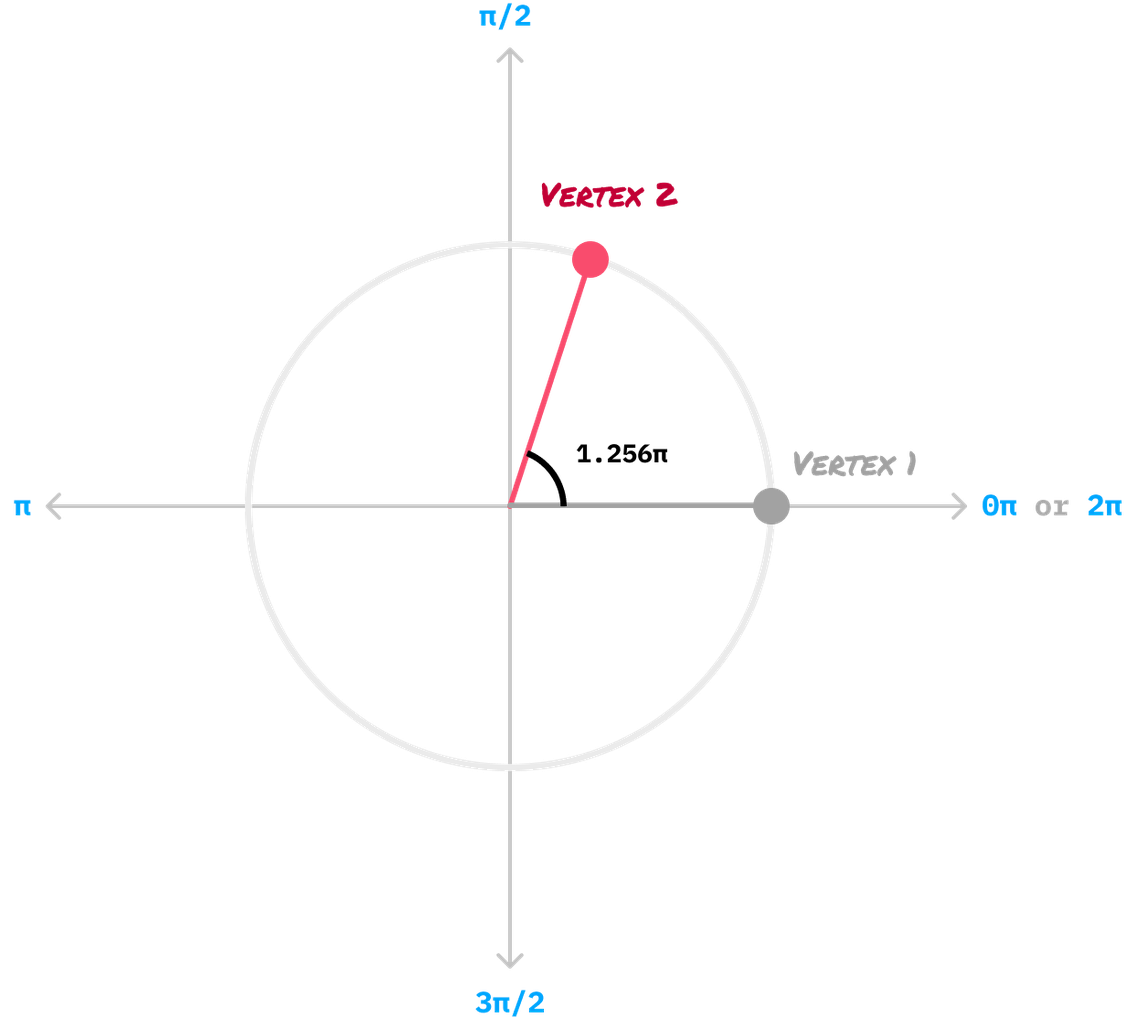
From here, we are one step closer to placing our vertices on the circle. Our next step requires a little bit of math, where we calculate the vertex angle. We find this angle by dividing the number of total vertices in our shape by the total number of radians in our circle, which is 2π. For our pentagon, the calculation will look as follows:
With our vertex angle now in hand, it is time to define our vertices. The first vertex will always be at an angle of 0 radians:
Each subsequent vertex will stay along this virtual circle path. The only variation will be the angle they are drawn in where each vertex is a multiple of the 1.256 angle we calculated earlier. Below is how Vertex 2 appears where it is drawn at an angle of 1.256 radians:
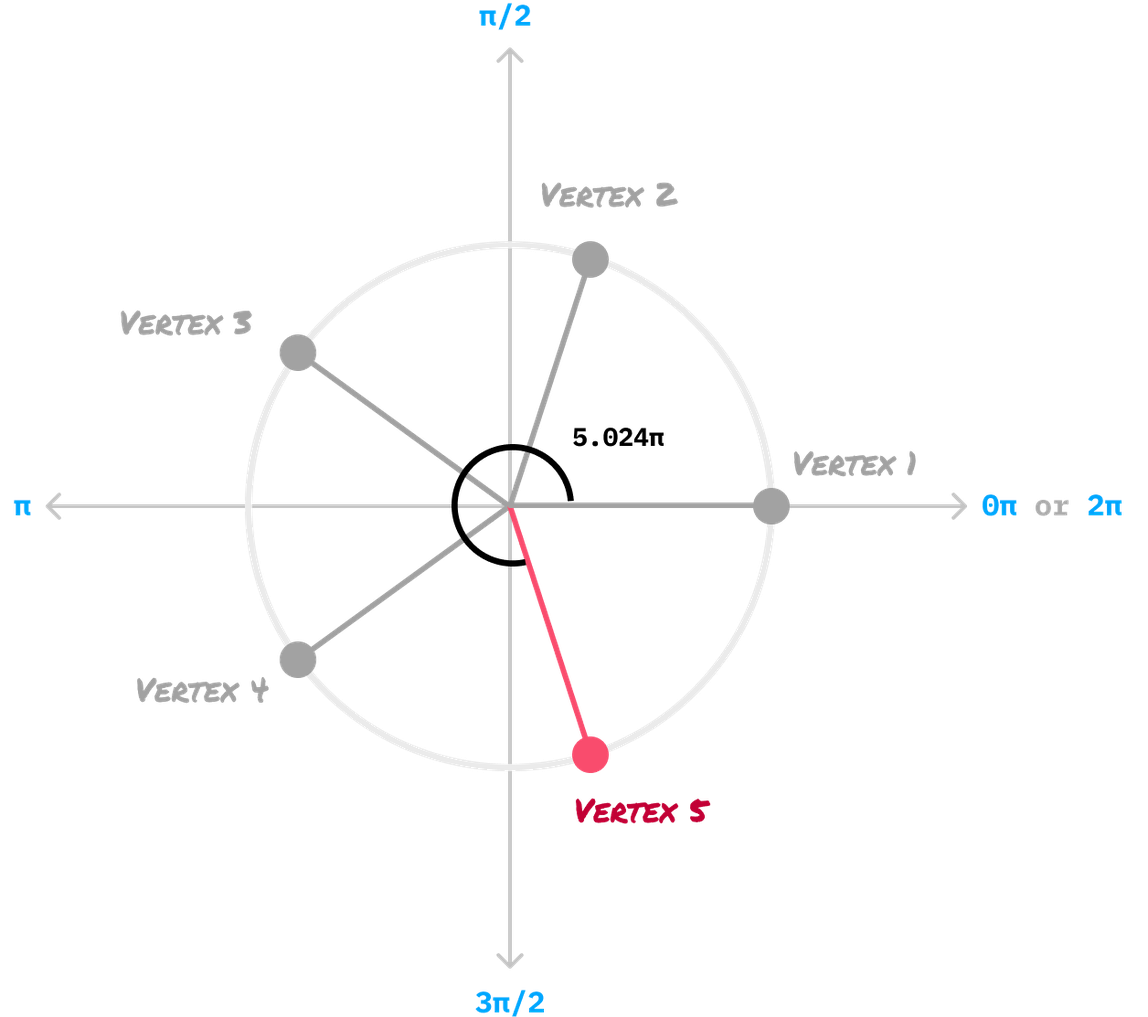
This process repeats itself for the other vertices in our polygon, where each vertex has its angle value incremented by another 1.256. This all stops with our final vertex, Vertex 5:
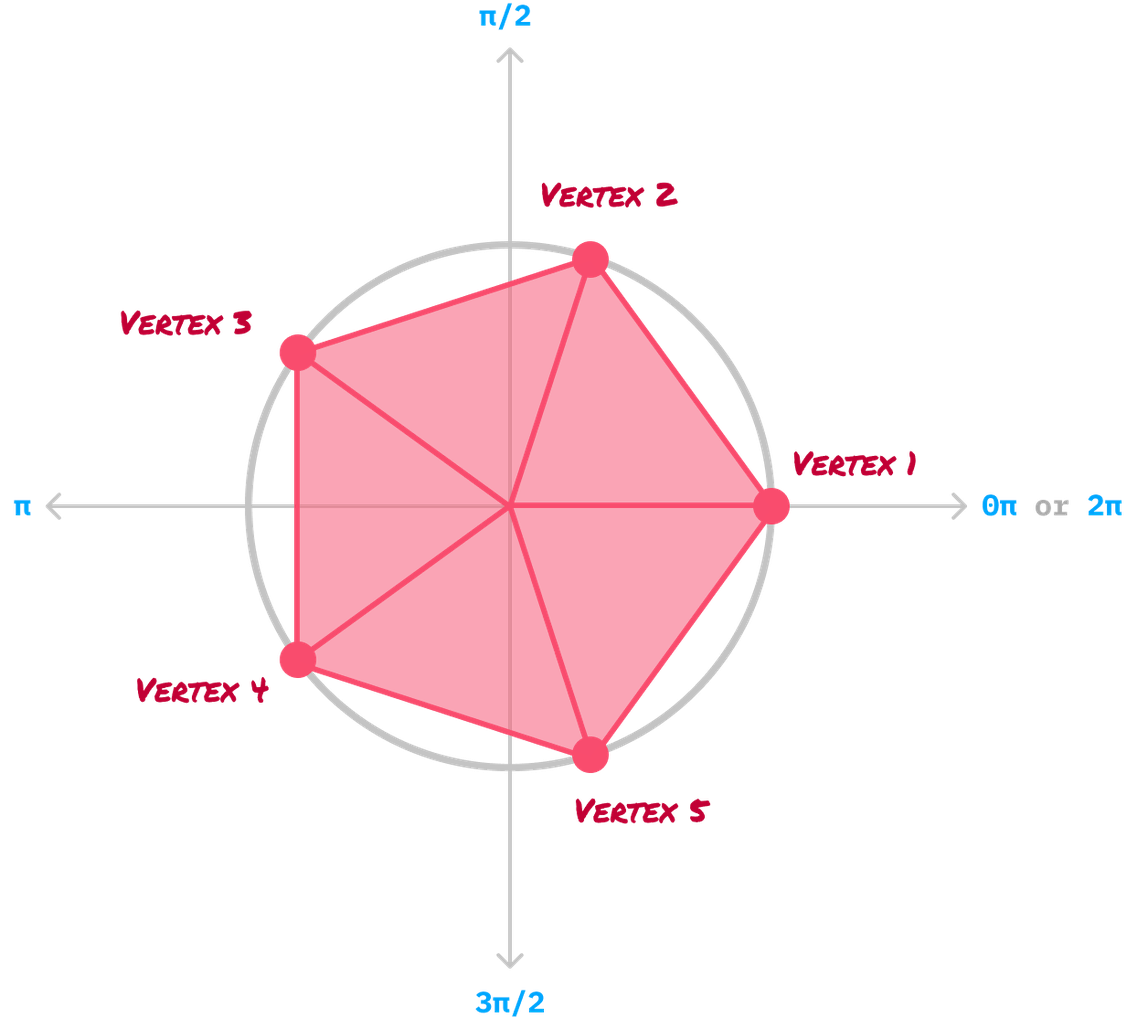
Just like our other vertices, Vertex 5 is positioned on our virtual circle. Its exact position is determined by its angle, which is 4 times 1.256 or...5.024. Putting this all together, the end result of all of our vertices being drawn looks as follows:
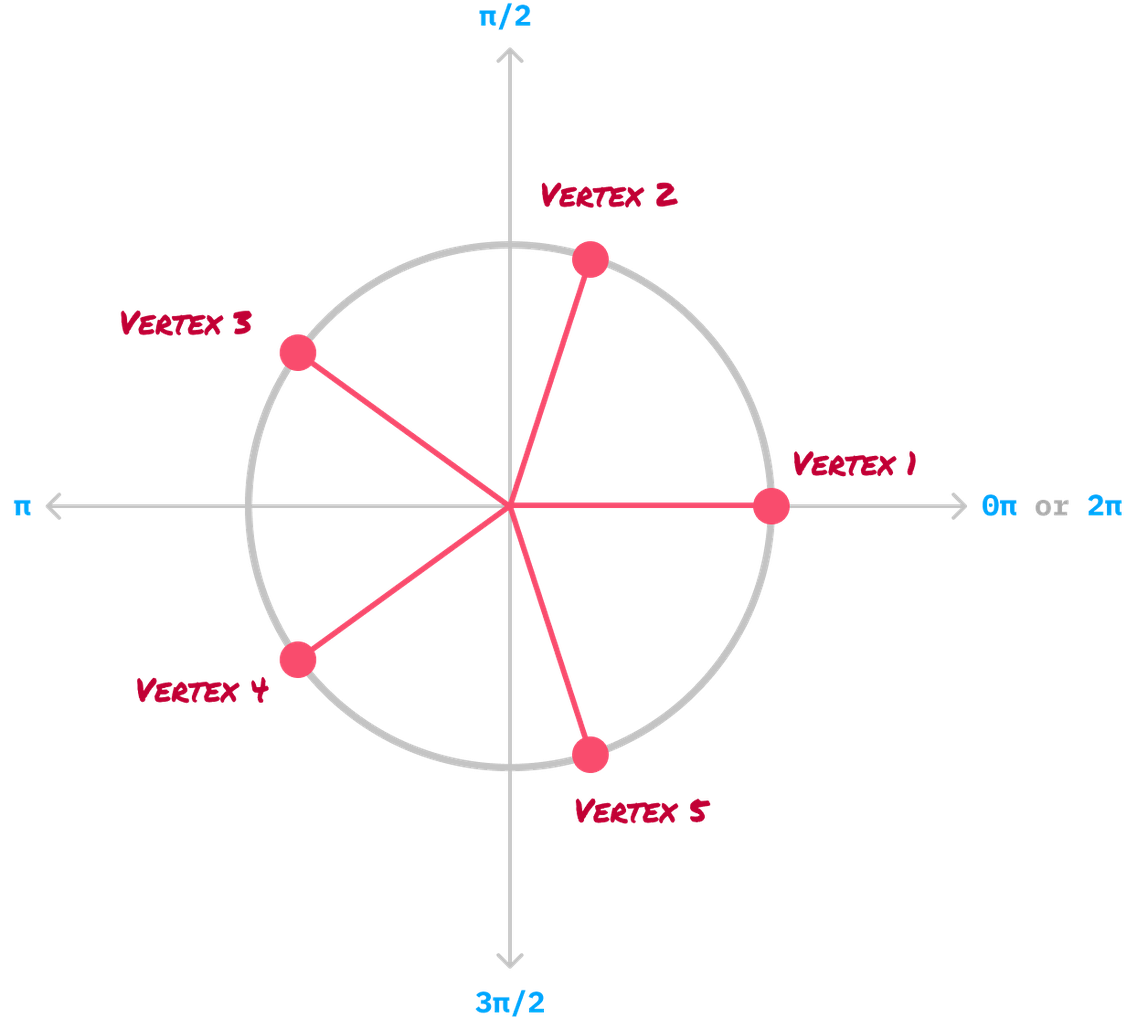
Our last step is to connect the vertices together with a straight line. When we do this for our pentagon, the final shape will emerge:
When we remove all of our guide lines and and extraneous markings, we’ll be left with a professional-looking version of the pentagon that we started off this entire exercise with.
The Code
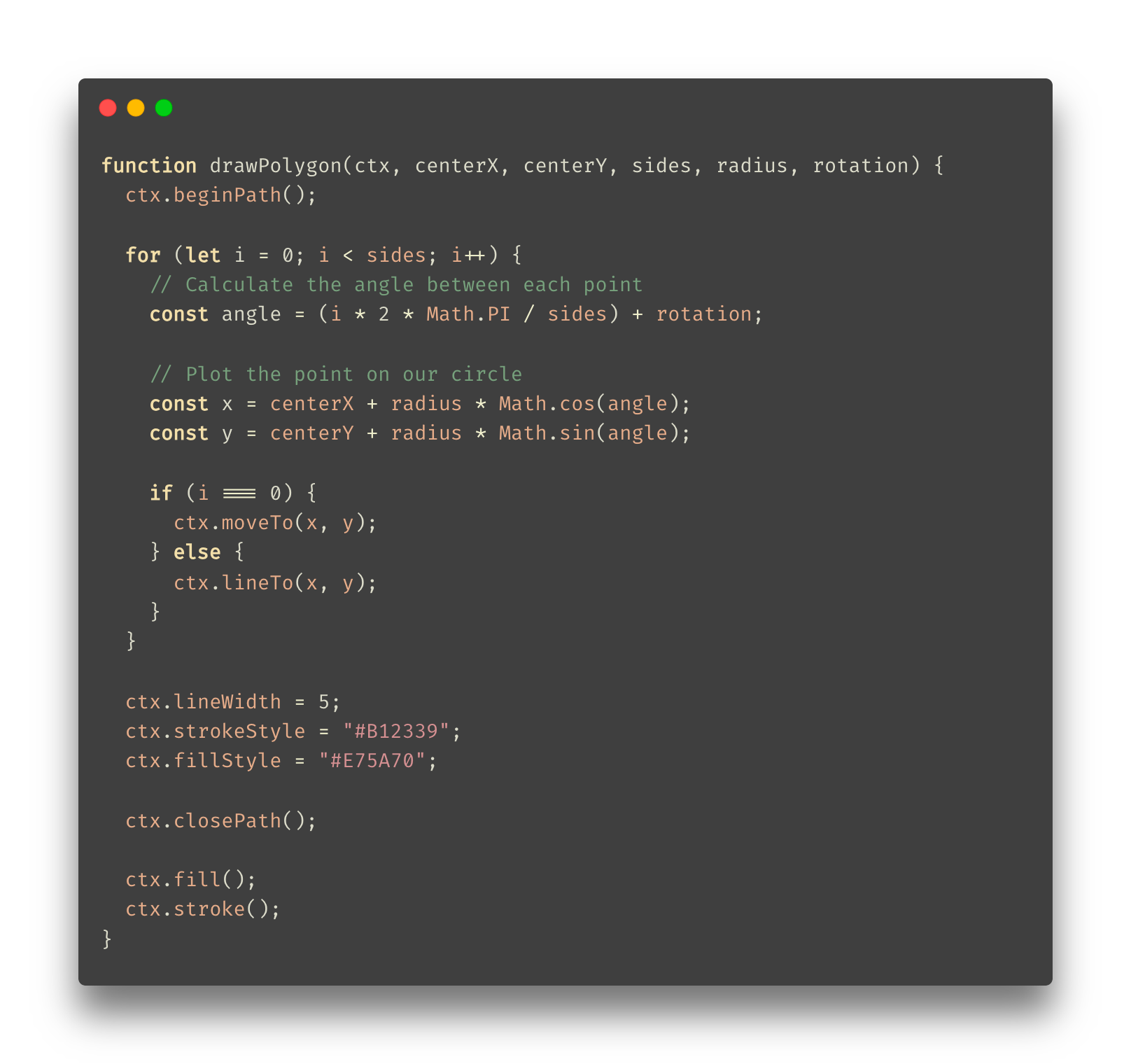
Now that we’ve seen our generalized approach for drawing our pentagon shape, all that remains is turn all of this knowledge into lines of code our browser can understand. Meet the drawPolygon function:
Take a few moments to walk through this code and see how we generate our vertices and connect them into a fully finalized shape. To see a fully working example of our drawPolygon function to draw our pentagon, take a look at the following CodePen example!
Conclusion
In code, there is always a generalized solution for any specific problem we are trying to solve. Generalized solutions tend to be more complex and difficult to reason than a very pinpointed solution. What we saw here is no example. To draw a familiar shape like a pentagon or a triangle, we looked at several pages of explanations and background detail. As developers, it is important to balance simplicity with generalizability, so be sure to keep this in mind the next time you are writing some code meant for broader reuse.
As always, thanks for being a subscriber! If you found this content useful, please share this newsletter with your network by retweeting this tweet:
To reach me, reply to this newsletter, post on the forums, or use carrier pigeons…if that is your thing! Just point those birds towards Seattle, and I’ll find them.
Cheers,
Kirupa 😇





I wish I had known about or thought of this approach a long time ago!